Solutions Class 12
Homogenous mixture
The homogenous mixture we mean that its composition and properties are uniform throughout the mixture.
Solutions
Solutions are homogeneous mixtures of two or more than two components.
Solvent
The component that is present in the largest quantity in the solution is known as
solvent. Solvent determines the physical state in which solution exists.
Solute
The component present in a smaller quantity in the solution other than solvent
is called the solute.
Binary solutions
Binary solutions i.e., consisting of two components.
Types of Solutions
- Gaseous Solutions
- Liquid Solutions
- Solid Solutions
Composition of a Solution
The composition of a solution can be described by expressing its
concentration. It can be expressed as
i) qualitatively
ii) quantitatively
i) Qualitatively
Qualitatively we can say that the solution is dilute (i.e., relatively
very small quantity of solute) or it is concentrated (i.e., relatively very
large quantity of solute).
ii) Quantitatively
There are several ways by which we can describe the concentration of the
solution quantitatively.
a) Mass percentage (w/w)
b) Volume percentage (V/V)
c) Mass by volume percentage (w/V)
d) Parts per million
e) Mole fraction
f) Molarity
g) Molality
a) Mass percentage (w/w): The mass percentage of a component of a
solution is defined as:
Mass % of a component
b) Volume percentage (V/V): The volume percentage is defined as:
c) Mass by volume percentage (w/V):
It is the mass of solute dissolved in 100 mL of the
solution.
d) Parts per million:
It is the parts of a component per million `(10^6)` parts of the solution.
Concentration in parts per million
can also be expressed as mass to mass, volume to volume and
mass to volume. A litre of sea water (which weighs 1030 g) contains
about `6 × 10^{–3}` g of dissolved oxygen (`O_2`). Such a small
concentration is also expressed as 5.8 g per `10^6`g (5.8 ppm) of sea
water.
Mass % of `O_2 = \frac {6\times 10^{-3}}{1030}\times 100 = 5.8 \times 10^{-4} %`
ppm of `O_2 = \frac {6\times 10^{-3}}{1030} \times 10^6 = 5.8` ppm
e) Mole fraction
The symbol for mole fraction is `x` and
subscript used on the right hand side of `x` denotes the component.
It is defined as:
👉 In a binary mixture, if the number of moles of `A` and `B` are `n_A` and `n_B` respectively, the mole fraction of `A` will be
`x_A = \frac{n_A}{n_A + n_B}`
👉 For a solution containing `i` number of components, we have:
`x_i = \frac{n_i}{n_1 + n_2 + n_3 ..+ n_i} = \frac{n_i}{\sum n_i}`
f) Molarity (M) is defined as number of moles of solute
dissolved in one litre (or one cubic decimetre) of solution
For example, `0.25 mol L^{–1} (or 0.25 M)` solution of NaOH means that
0.25 mol of NaOH has been dissolved in one litre.
g) Molality (m) is defined as the number of moles of the
solute per kilogram (kg) of the solvent and is expressed as:
Solubility
👉The solubility of a substance is its maximum amount that can be dissolved
in a specified amount of solvent at a specified temperature.
It depends
upon the nature of solute and solvent as well as temperature and
pressure.
Solubility of a Solid in a Liquid
Every solid does not dissolve in a given liquid.
👉 Polar solutes dissolve in polar solvents and non-polar solutes in non-polar solvents.
In general, a solute dissolves in a solvent if the
intermolecular interactions are similar in the two or we may say like
dissolves like.
Examples:
👉 Sodium chloride
and sugar dissolve readily in water
👉 Naphthalene and anthracene do
not dissolve in water
👉 Naphthalene and anthracene dissolve readily in
benzene.
👉 Sodium chloride and sugar do not.
Dissolution
👉When a solid solute is added to the solvent, some solute dissolves
and its concentration increases in the solution. This process is known as
dissolution.
Saturated solution
👉Such a solution in which no more solute can be dissolved at the same
temperature and pressure is called a saturated solution.
Unsaturated solution
An
unsaturated solution is one in which more solute can be dissolved at
the same temperature
Effect of temperature on solubility
The solubility of a solid in a liquid is significantly affected by temperature
changes.
Effect of pressure
Pressure does not have any significant effect on the solubility of solids in
liquids. It is so because solids and liquids are highly incompressible
and practically remain unaffected by changes in pressure.
Solubility of a Gas in a Liquid
Solubility of gases in liquids is greatly affected by pressure and temperature. The solubility of gases increase with increase of pressure
Consider a system as shown in
Fig. (a). The lower part is solution and the upper part is gaseous
system at pressure `p` and temperature `T`. Assume this system to be in
a state of dynamic equilibrium, i.e., under these conditions rate of
gaseous particles entering and leaving the solution phase is the same.
Now increase the pressure over the solution phase by compressing the
gas to a smaller volume [Fig. (b)]. This will increase the number of
gaseous particles per unit volume over the solution.
👉 Quantitative relation between
pressure and solubility of a gas
in a solvent which is known as
Henry’s law.
Henry's Law
The
solubility of a gas in a liquid
is directly proportional to the
partial pressure of the gas
present above the surface of
liquid or solution.
Or
The partial pressure of the gas
in vapour phase `(p)` is proportional to the mole fraction
of the gas `(x)` in the solution.
`p = K_H x`
Here `K_H` is the Henry’s law constant.
👉 Different gases have different `K_H` values at the same
temperature . This suggests that `K_H` is a
function of the nature of the gas.
👉 It is obvious from equation `p = K_H x` that higher the
value of `K_H` at a given pressure, the lower is the solubility
of the gas in the liquid.
Vapour Pressure of Solutions
The pressure exerted by the vapours above the liquid surface in equilibrium with the liquid at a given temperature is called vapour pressure
Raoult’s law
For a solution of volatile liquids, the partial vapour pressure of each component of the solution
is directly proportional to its mole fraction present in solution.
Thus, for component 1
`p_1 ∝ x_1`
and `p_1 = p_1^0 x_1`
where `p_1^0 ` is the vapour pressure of pure component 1 at the same
temperature
Similarly, for component 2
`p_2 = p_1^0 x_2`
where `p_2^0 ` is the vapour pressure of pure component 2 at the same temperature
According to Dalton’s law of partial pressures, the total pressure `( p_t )` over the solution phase in the container will be the sum of the
partial pressures of the components of the solution and is given as:
`p_t = p_1 +p_2`
Substituting the values of `p_1` and `p_2`, we get
`p_t = x_1p_1^0 + x_2 p_2^0`
`= (1 - x_2)p_1^0 + x_2 p_2^0`
` = p_1^0 + (p_2^0 - p_1^0)x_2`
A plot of `p_1` or `p_2` versus the mole
fractions `x_1` and `x_2` for a solution gives a
linear plot as shown in Fig.
👉 The composition of vapour phase in
equilibrium with the solution is determined
by the partial pressures of the components.
If `y_1` and `y_2` are the mole fractions of the components 1 and 2 respectively in the vapour phase then, using Dalton’s
law of partial pressures:
`p_1 = y_1p_t`
`p_2 = y_2p_t`
Raoult’s Law as a special case of Henry’s Law
In the solution of a gas in a
liquid
According to Raoult’s Law
`p_1 = x_1p_1^0`
According to Henry’s Law
`p = K_H x`
Only the
proportionality constant `K_H` differs from `p_1^0` . Thus, Raoult’s law becomes
a special case of Henry’s law in which `K_H = p_1^0` .
Vapour
Pressure of
Solutions of
Solids in
Liquids
This vapour pressure of the
solution at a given temperature is found to
be lower than the vapour pressure of the
pure solvent at the same temperature.
In
the solution, the surface has both solute and
solvent molecules; thereby the fraction of the
surface covered by the solvent molecules gets
reduced. Consequently, the number of
solvent molecules escaping from the surface
is correspondingly reduced, thus, the vapour
pressure is also reduced.
The decrease in the vapour pressure of solvent depends on the
quantity of non-volatile solute present in the solution, irrespective of
its nature. For example, decrease in the vapour pressure of water by
adding 1.0 mol of sucrose to one kg of water is nearly similar to that
produced by adding 1.0 mol of urea to the same quantity of water at
the same temperature.
In a binary solution, let us denote the solvent by 1 and solute by
2. When the solute is non-volatile, only the solvent molecules are
present in vapour phase and contribute to vapour pressure.
Let `p_1` be the vapour pressure of the solvent, `x_1` be
its mole fraction, `p_1^0` be its vapour pressure
in the pure state. Then according to
Raoult’s law
`p_1 \propto x_1`
The proportionality constant is equal
to the vapour pressure of pure solvent, `p_1^0` .
A plot between the vapour pressure and
the mole fraction of the solvent is linear.
Ideal Solutions
The solutions which obey Raoult’s law over the entire range of
concentration are known as ideal solutions.
The ideal solutions have
two other important properties.
👉The enthalpy of mixing of the pure
components to form the solution is zero
`Delta_{mix} H = 0`
👉 The volume of mixing is
also zero.
`Delta_{mix} V = 0`
It means that no heat is absorbed or evolved when the components
are mixed. Also, the volume of solution would be equal to the sum of
volumes of the two components.
At molecular level, ideal behaviour of the solutions
Considering two components A and
B. In pure components, the intermolecular attractive interactions will
be of types A-A and B-B, whereas in the binary solutions in addition
to these two interactions, A-B type of interactions will also be present.
If the intermolecular attractive forces between the A-A and B-B are
nearly equal to those between A-B, this leads to the formation of ideal
solution.
👉Examples: Solution of n-hexane and n-heptane, bromoethane
and chloroethane, benzene and toluene, etc. fall into this category.
Non-ideal Solutions
When a solution does not obey Raoult’s law over the entire range of
concentration, then it is called non-ideal solution.
The vapour pressure
of such a solution is either higher or lower than that predicted by
Raoult’s law. If it is higher, the solution exhibits positive
deviation and if it is lower, it exhibits negative deviation from Raoult’s
law.
The cause for these deviations
Positive Deviation
The cause for these deviations lie in the nature of interactions at the
molecular level.
A-B
interactions are weaker than those between A-A or B-B, i.e., in this case
the intermolecular attractive forces between the solute-solvent molecules
are weaker than those between the solute-solute and solvent-solvent
molecules. This means that in such solutions, molecules of A (or B) will
find it easier to escape than in pure state. This will increase the vapour pressure and result in positive deviation.
Mixtures of ethanol and acetone
behave in this manner.
Negative Deviation
In case of negative deviations from Raoult’s law, the intermolecular
attractive forces between A-A and B-B are weaker than those between
A-B and leads to decrease in vapour pressure resulting in negative
deviations.
Colligative Properties
👉The properties of solutions which depend on the number of solute particles and
are independent of their chemical identity are called colligative properties.
Four important colligative propertie are:
(1) relative lowering of vapour
pressure of the solvent
(2) depression of freezing point of the solvent
(3) elevation of boiling point of the solvent and
(4) osmotic pressure of
the solution.
(1) Relative lowering of vapour pressure of the solvent
Non-volatile solute in a solution.
The vapour pressure of
the solution, mole fraction and vapour pressure of the solvent, i.e.
`p_1 = x_1p_1^0`
The reduction in the vapour pressure of solvent `(∆p_1)` is given as:
`∆p_1 = p_1^0 - p_1 = p_1^0 - p_1^0 x_1`
`= p_1^0(1-x_1)`
`\Delta p_1 = x_2 p_1^0`
Equation can be written as
`\frac {\Delta p_1}{p_1^0} = \frac {p_1^0 - p_1}{p_1^0} = x_2`
Relative lowering of vapour pressure and is equal to
the mole fraction of the solute.
`\frac {p_1^0 - p_1}{p_1^0} = \frac {n_2}{n_1 +n_2} (∵ x_2 = \frac {n_2}{n_1 +n_2})`
Here `n_1` and `n_2` are the number of moles of solvent and solute
respectively present in the solution. For dilute solutions `n_2 < < n_1`,
hence neglecting `n_2` in the denominator we have
`frac {p_1^0 - p_1}{p_1^0} = \frac {n_2}{n_1}`
or
`frac {p_1^0 - p_1}{p_1^0} = \frac {w_2 \times M_1}{M_2\times w_1}`
From this equation , knowing all other quantities, the molar
mass of solute `(M_2)` can be calculated.
Elevation of Boiling Point
The vapour pressure of a
liquid increases with increase of temperature. It boils at the
temperature at which its vapour pressure is equal to the atmospheric
pressure. For example, water boils at `373.15 K` `(100° C)` because at
this temperature the vapour pressure of water is `1.013` bar (1
atmosphere).
The vapour
pressure of the solvent decreases in the presence of a non-volatile solute.
For example, the vapour
pressure of an aqueous solution of sucrose is less than `1.013` bar at `373.15 K.` In order to make this solution boil, its vapour pressure
must be increased to `1.013` bar by raising the temperature above the
boiling temperature of the pure solvent (water). Thus, the boiling point of a solution is always higher than that of
the boiling point of the pure solvent in which the
solution is prepared as shown in Fig.
Let `T_b^0` be the boiling point of pure solvent and `T_b` be the boiling point of solution.
👉 The increase in
the boiling point `∆T_b = T_b - T_b^0` is known as
elevation of boiling point.
For dilute
solutions the elevation of boiling point `(∆Tb)` is
directly proportional to the molal concentration of
the solute in a solution. Thus
`∆Tb \propto m`
Or,
`∆Tb = K_b m`
Here `m` (molality) is the number of moles of solute dissolved in 1 kg
of solvent and the constant of proportionality, `K_b` is called Boiling Point
Elevation Constant or Molal Elevation Constant (Ebullioscopic
Constant). The unit of `K_b` is `K kg mol^{-1}`.
Osmosis
The phenomenon of the flow of solvent through a semi-permeable membrane from pure solvent (or dilute solution) to the solution (or concentrated solution) is called osmosis.
Semipermeable Membranes (SPM)
Small solvent molecules, like water, can pass through these holes but the passage of
bigger molecules like solute is hindered. Membranes having this kind
of properties are known as semipermeable membranes (SPM).
Osmotic Pressure `(\Pi)`
The osmotic pressure of a solution is the
excess pressure that must be applied to a
solution to prevent osmosis, i.e., to stop the
passage of solvent molecules through a
semipermeable membrane into the solution.
Osmotic pressure is a
colligative property as it depends on the number
of solute molecules and not on their identity.
`\Pi = CRT`
Here `Pi` is the osmotic pressure and `R` is the
gas constant
`\Pi = (\frac {n_2}{V})RT`
Here `V` is volume of a solution in litres containing `n_2` moles of solute.
If `w_2` grams of solute, of molar mass, `M_2` is present in the solution, then `n_2
= w_2
/ M_2` and we can write,
`\Pi V = \frac {w_2RT}{M_2}`
or `M_2= \frac {w_2RT}{\Pi V}`
Thus, knowing the quantities `w_2
, T, Π` and `V` we can calculate the
molar mass of the solute.
Isotonic Solutions
Two solutions having same osmotic pressure at a given
temperature are called isotonic solutions.
When such solutions
are separated by semipermeable membrane no osmosis occurs
between them.
For example, the osmotic pressure associated with
the fluid inside the blood cell is equivalent to that of 0.9% (mass/
volume) sodium chloride solution, called normal saline solution and
it is safe to inject intravenously.
Hypertonic Solutions
If we place the
cells in a solution containing more than 0.9% (mass/volume) sodium
chloride, water will flow out of the cells and they would shrink. Such
a solution is called hypertonic.
Hypotonic solutions
If the salt concentration is less than
0.9% (mass/volume), the solution is said to be hypotonic. In this
case, water will flow into the cells if placed in this solution and they
would swell.
Reverse Osmosis and Water Purification
The direction of osmosis can be reversed if a pressure larger than the
osmotic pressure is applied to the solution side. That is, now the
pure solvent flows out of the solution through the semipermeable
membrane. This phenomenon is called reverse osmosis
Reverse osmosis is used in the desalination of sea
water. A schematic set up for the process is shown in Fig.
When pressure more than osmotic pressure is
applied, pure water is squeezed out of the sea
water through the membrane.
The pressure required for reverse osmosis
is quite high. A workable porous membrane is a
film of cellulose acetate placed over a suitable
support. Cellulose acetate is permeable to water
but impermeable to impurities and ions present
in sea water.






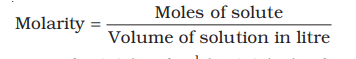












Nice
ReplyDeleteWonderful 📝
ReplyDeleteThank you
DeleteApka notes se concept or mind dono clear ho jta hai 😇😇
ReplyDeleteNice
ReplyDeleteVery nice notes
ReplyDelete